Wenn Sie für einen bestimmten Zeitraum monatlich einen festen Betrag anlegen möchten, ist es interessant zu erfahren, wie hoch in Abhängigkeit von der monatlichen Sparrate das Kapital am Ende des Zeitraums ist und wie viel Zinsen Sie erwirtschaftet haben.
Die Funktion ZW aus der Kategorie der finanzmathematischen Funktionen eignet sich für die Berechnung des Endkapitals unter der Voraussetzung, dass der Zinssatz und der regelmäßige Sparbetrag über den gesamten Zeitraum konstant bleiben.
Beispiel
Wenn Sie über 5 Jahre monatlich einen Betrag von 50 € ansparen und der vereinbarte Zinssatz 3% p.a. lautet, verfügen Sie am Ende über einen Betrag in Höhe von 3.232,34 €. Die Zinsen werden bei diesem Beispiel monatlich gutgeschrieben.
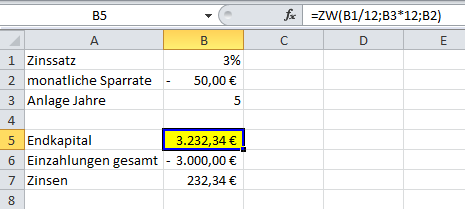
Das Endkapital in Zelle B5 wird mit der Funktion ZW folgendermaßen berechnet:
=ZW(Zinssatz pro Periode;Anzahl Zahlungen;Sparbetrag)
=ZW(B1/12;B3*12;B2)
Die Sparrate in Zelle B2 wird mit einem negativen Vorzeichen eingegeben, weil es sich um eine Auszahlung handelt. Da sich der Zinssatz von 3% in Zelle B1 auf ein Jahr bezieht, muss er auf den Monat umgerechnet und daher durch 12 dividiert werden.
Die Höhe der Einzahlungen in Zelle B6 ergibt sich aus der Multiplikation des Sparbeitrags mit der Anzahl der Zahlungen. Die erwirtschafteten Zinsen in Zelle B7 errechnen sich durch die Differenz zwischen dem Endkapital und der Summe der geleisteten Zahlungen.
Um sich einen Überblick zu verschaffen, wie sich die Höhe der monatlichen Sparrate auf das jeweilige Endkapital und die Zinsen auswirkt, kann in Excel eine Datentabelle eingesetzt werden.
Die Datentabelle hat folgenden Aufbau:
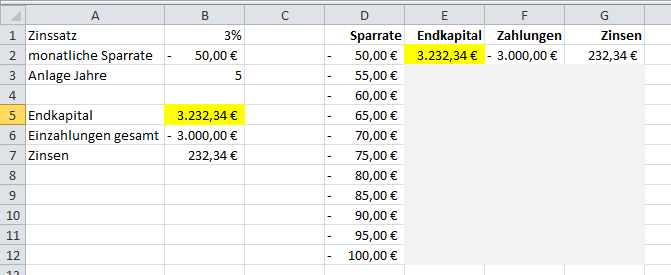
Folgende Formeln wurden eingegeben:
| Zelle | Formel |
| D2 | =B2 |
| E2 | =B5 |
| F2 | =B6 |
| G2 | =B7 |
Um das Endkapital, die Summe der Einzahlungen und Zinsen für diverse monatliche Sparraten zu ermitteln, gehen Sie bitte folgendermaßen vor:
- Markieren Sie den Zellbereich D2:G12.
-
Klicken Sie im Menüband auf der Registerkarte Daten in der Gruppe Datentools auf die Schaltfläche Datentabelle. Die Datentabelle gehört zu den sog. Was-wäre-wenn-Analysen. Das folgende Dialogbild erscheint:
- Klicken Sie in das Textfeld Werte aus Spalte. Aktivieren Sie die Zelle B2. Sie enthält die für die ursprüngliche Berechnung des Endkapitals herangezogene monatliche Sparrate. Der Zellbezug wird in das Textfeld übertragen.
- Klicken Sie auf die Schaltfläche OK.
Das Ergebnis sieht folgendermaßen aus:
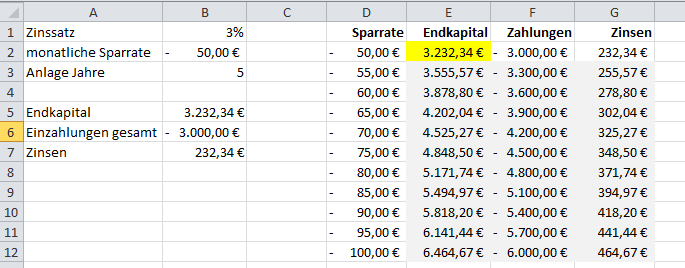
In den Zellen E3:G12 wurde folgende Matrix- bzw. Arrayformel eingetragen:
{=MEHRFACHOPERATION(;B2)}
Sie berechnet eine Formel mehrfach, indem sie den Wert, der in Zelle B2 steht, nacheinander durch die Werte ersetzt, die in der ersten Spalte des markierten Zellbereichs stehen.
Hinweise
- Beim Einsatz einer Datentabelle ist die Zelle B2 besonders wichtig. Sie muss entweder die ursprüngliche Formel enthalten oder einen Zellbezug zu einer Formel aufweisen.
- In dem Dialogbild Datentabelle wurde der Zellbezug B2 in dem Textfeld Werte aus Spalte eingetragen, weil die diversen Sparraten in einer Spalte untereinander stehen.
- Der Zellbereich mit den Matrixformeln ist ein geschützter Bereich, d.h. Sie können weder Zeilen oder Spalten einfügen bzw. löschen noch einzelne Formeln löschen oder ändern.
- Wenn Sie den Zinssatz bzw. die Anzahl der Jahre ändern, werden alle Beträge neu errechnet.

Wie kann man denn die Laufzeit berechnen.
Ich habe ein Sparziel (in R6), Aktuelles Vermögen (inS6), Monatliche Rate (in O6) und den Jährlichen Zins (in T6)
Wie kann man die Restlaufzeit in Monaten ausrechnen?
Hallo Herr Möllmann,
versuchen Sie es mit folgender Formel:
=ZZR(T6/12;O6;S6;R6)
Zeitersparnis
Falsche Berechnung, da hier mit 3 % p. m. und nicht pro jahr gerechnet wird
Nein, der Zinssatz wird nicht falsch berechnet. Wegen der monatlichen Kapitalisierung wurde der Zins ja durch 12 (Monate) geteilt. Was allerdings die Formel unbrauchbar macht, ist die monatliche Zinskapitalisierung bei einem Ansparprodukt. Das gibt es bei keiner Bank.